Using the summary file of the Million Song Dataset, how can we find out the average BPM of tracks per year? (This is an IPython notebook showing how to start working with the MSD. See the original gist to download.)
First, let's import the PyTables module, then open up the file (available from http://labrosa.ee.columbia.edu/millionsong/sites/default/files/AdditionalFiles/msd_summary_file.h5).
import tables
h5file = tables.openFile("msd_summary_file.h5")
Let's see what the file's structure is like.
h5file
We want to find songs in each year (/musicbrainz/songs/year) and to retrieve the BPM (/analysis/songs/tempo) for each one.
musicbrainz = h5file.root.musicbrainz.songs
analysis = h5file.root.analysis.songs
from collections import defaultdict
by_year = defaultdict(list)
for row1 in musicbrainz.where('year != 0'):
row2 = analysis[row1.nrow]
by_year[row1['year']].append(row2['tempo'])
print("Year\tAvg. BPM")
for year, values in by_year.iteritems():
num_songs = len(values)
print("{}\t{:0.2f} ({} songs)".format(year, float(sum(values))/num_songs, num_songs))
A little sparse before 1953, but we'l take it. Now let's see what the trend is (if any).
We'll fit a LOWESS curve, then plot both it and the raw means.
# lowess function from https://gist.github.com/agramfort/850437
import numpy as np
from math import ceil
from scipy import linalg
def lowess(x, y, f=2./3., iter=3):
"""lowess(x, y, f=2./3., iter=3) -> yest
Lowess smoother: Robust locally weighted regression.
The lowess function fits a nonparametric regression curve to a scatterplot.
The arrays x and y contain an equal number of elements; each pair
(x[i], y[i]) defines a data point in the scatterplot. The function returns
the estimated (smooth) values of y.
The smoothing span is given by f. A larger value for f will result in a
smoother curve. The number of robustifying iterations is given by iter. The
function will run faster with a smaller number of iterations."""
n = len(x)
r = int(ceil(f*n))
h = [np.sort(np.abs(x - x[i]))[r] for i in range(n)]
w = np.clip(np.abs((x[:,None] - x[None,:]) / h), 0.0, 1.0)
w = (1 - w**3)**3
yest = np.zeros(n)
delta = np.ones(n)
for iteration in range(iter):
for i in range(n):
weights = delta * w[:,i]
b = np.array([np.sum(weights*y), np.sum(weights*y*x)])
A = np.array([[np.sum(weights), np.sum(weights*x)],
[np.sum(weights*x), np.sum(weights*x*x)]])
beta = linalg.solve(A, b)
yest[i] = beta[0] + beta[1]*x[i]
residuals = y - yest
s = np.median(np.abs(residuals))
delta = np.clip(residuals / (6.0 * s), -1, 1)
delta = (1 - delta**2)**2
return yest
%matplotlib notebook
import matplotlib.pyplot as plt
x = np.arange(1950, 2010)
y = np.array([np.mean(by_year[i]) for i in x])
# need to rescale, else we get a singular matrix
scaled_x = np.arange(0,1, 1.0/len(x))
ymax = float(np.max(y))
scaled_y = y / ymax
f = 0.25 # smoothing span; larger == smoother
yest = lowess(scaled_x, scaled_y, f=f, iter=3)
yest *= ymax
plt.xlim(1950, 2010)
plt.scatter(x, y, label='y raw')
plt.plot(x, yest, label='y smoothed')
plt.xlabel('year')
plt.ylabel('Average BPM')
plt.title('BPMs over time')
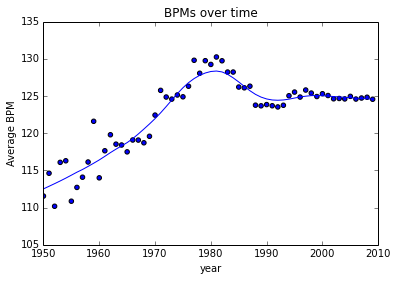
The tendency seems to have been a gradual increase since the '50s (when the data goes over 100 samples), peaking at 130 BPM in 1981 and settling around 124 BPM. Of course, these numbers should be treated with some skepticism, as 1993-2009 are significantly overrepresented in the corpus.